Gdybyś miał do wyboru tylko jeden rodzaj wykresu, którego mógłbyś użyć do zrozumienia znaczenia danych, tak aby uzyskana informacja mogła zostać wykorzystana do podjęcia działania i rozwiązania problemu, to który byś wybrał?
Histogram, time series plot, scatterplot, dotplot, control chart, normal probability plot, a może box plot?
Nawiązując do powyższego pytania, przedstawię Ci jeden rodzaj wykresu, dzięki któremu w 90% przypadków będziesz w stanie znaleźć sygnały w danych i podjąć konkretne działania, zbliżające Cię do rozwiązania problemu.
Oprócz wspomnianego wykresu pokażę Ci też 4 inne, bez których obejść się nie można.
To wynik mojego doświadczenia w realizowaniu projektów doskonalących oraz jako mentora dla wielu Six Sigma Green i Black Beltów.
Zanim jednak przeczytasz ten artykuł, zapoznaj się z moim poprzednim wpisem:
Zawartość artykułu
Jaki jest cel graficznej analizy danych?
Zanim przedstawię Ci wspomniane wykresy, musimy sobie najpierw odpowiedzieć na pytanie:
Jaki jest cel graficznej analizy danych?
Celem graficznej prezentacji danych jest odseparowanie wszelkich sygnałów od szumu występującego w tych danych oraz wykorzystanie możliwości wizualnych do skutecznego przekazywania znalezionych sygnałów.
W tym poście skupimy się tylko na skutecznym znajdowaniu sygnałów w danych, a nie na efektywnej prezentacji danych.
Jeśli jesteś zainteresowany efektywną prezentacją danych, to zarejestruj się do newslettera i odbierz darmowy ebook.
"Aby znaleźć sygnały w danych, musimy nauczyć się redukować szum - nie tylko szum, który rezyduje w danych, ale także szum, który rezyduje w nas samych. Dla hałaśliwych umysłów jest prawie niemożliwe, aby dostrzec w danych coś poza szumem."
Stephen Few, Signal: Understanding What Matters in a World of Noise
Podjęcie decyzji, którego wykresu użyć...
Wybór danego wykresu zależy od pytania, które stawiamy:
- „Jakie są główne źródła zmienności w procesie?”
- „Jak proces zachowuje się w czasie?”
- „Czy jest różnica między dostawcą A, a dostawcą B?”
- „Jaki jest rozkład danych z mojego procesu?”
- „Czy istnieje zależność między dwoma (lub więcej) zmiennymi?”
- „Czy mogę ufać mojemu systemowi pomiarowemu?”
- „Czy istnieje efekt systematyczny/sezonowy?”
- „Jaki jest efekt zmiany konkretnych czynników na wyjście procesu?”
W kontekście graficznej prezentacji danych pytania sprowadzają się zasadniczo do czterech typów:
- Porównanie
- Kompozycja
- Rozkład
- Zależność
Istnieje diagram stworzony przez dr Andrew Abela, który może być pomocny w wyborze odpowiedniego wykresu.
(Wersję PDF można pobrać tutaj)

Przejdźmy zatem do rekomendowanej przeze mnie listy najbardziej użytecznych wykresów, które każdy menedżer, inżynier i praktyk projektów doskonalących znać powinien (nie tylko Six Sigma Green i Black Belt).
Wszystkie wykresy zostały stworzone w programie Minitab i pochodzą z rzeczywistych projektów doskonalących.
1. Individual Value Plot
Na miejscu pierwszym najważniejszy wykres dla każdego, kto rozwiązuje problemy, optymalizuje procesy i zajmuje się poprawą jakości.
To wykres, dzięki któremu ja i moi studenci są w stanie rozwiązać 90% problemów, zakładając, że wiemy jak zebrać odpowiedniej jakości dane.
Poniżej przedstawię Ci kilka przykładowych zastosowań Individual Value Plot.
Monitorowanie
Przykład:
Monitorujemy wymiar krytyczny komponentu wykonanego z tworzywa sztucznego wykonanego metodą wtrysku.
Każdego dnia mierzymy trzy sztuki i dane przedstawiamy na wykresie Individual Value Plot, na którym też nanosimy limity specyfikacji.

Interpretacja:
- Proces jest wycentrowany i wewnątrz limitów specyfikacji.
- Zmienność procesu jest około dwukrotnie mniejsza niż zakres tolerancji (górna granica specyfikacji – dolna granica specyfikacji).
- W procesie mamy do czynienia ze zmiennością naturalną – żaden z pomiarów wewnątrz prostokątów znacząco nie odstaje od reszty.
- Proces jest przewidywalny, co oznacza, że jeśli warunki się nie zmienią, to możemy oczekiwać podobnych wartości w przyszłości.
- Dominującym źródłem zmienności, jest zmienność część do części (trzy kropki wewnątrz prostokątów), ponieważ większość prostokątów zachodzi na siebie i jest mniej więcej na tym samym poziomie.
Badanie składników zmienności (Component of Variation Study)
Przykład 1:
Producent kulek do łożysk miał problem ze zmiennością odchyłek kulistości.
W celu zrozumienia głównych źródeł zmienności przeprowadziliśmy COV (ang. Component of Variation Study), czyli badanie składników zmienności.
Spośród wielu hipotez najbardziej prawdopodobną była ta, że głównym źródłem zmienności jest zmienność partia do partii.
W związku z tym zespół pobrał 3 kulki z 10 partii i zmierzył odchyłki kulistości.
Analizę danych możesz zobaczyć poniżej:

Interpretacja:
- Proces nie spełnia wymagań – przekroczone limity specyfikacji.
- Głównym źródłem zmienności, jest partia do partii – prostokąty wyraźnie skaczą między sobą.
- Zmienność wewnątrz partii jest zmiennością naturalną – żaden z pomiarów wewnątrz partii znacząco nie odstaje od reszty.
Po wytypowaniu na podstawie mapy procesu potencjalnych czynników i zakłóceń, które mogą być przyczyną zmienności partia do partii, zespół przeprowadził 3 planowane eksperymenty (Design of Experiments) i zredukował zmienność.
Wynik możesz zobaczyć poniżej:

Przykład 2
W laboratorium jednym z problemów była nadmierna zmienność przy oznaczeniach stężenia molibdenu w próbkach, które przygotowywane były poprzez rozpuszczenie odważek analitycznych molibdenianu amonu.
Zespół starał się zrozumieć główne źródła zmienności:
- Operator do operatora
- Naważka do naważki
- Próbka do próbki
- Pomiar do pomiaru

Interpretacja:
- Dominującym źródłem zmienności jest zmienność pomiar do pomiaru dla obu operatorów – dwa punkty wenwątrz prostokątów.
- Wyraźna różnica w zmienności pomiar do pomiaru pomiędzy operatorami – dla operatora nr 1 zmienność pomiar do pomiaru jest zdecydowanie większa, niż dla operatora nr 2.
- Zmienność pomiar do pomiaru (powtarzalność), jest przewidywalna dla obu operatorów.
- Wyraźne przesunięcie między operatorami (bias) – operator 2 ma wyższe średnie wyniki.
- Żadna z odważek nie dała stężenia roztworu o wartości 1g Mo/dm3 (problem dokładności).
Przykład 3
W tym przykładzie mamy Individual Vale Plot, w którym analizowane są cztery potencjalne źródła zmienności.
Problemem w tym przypadku była zbyt duża zmienność w kącie zagięcia stalowego panelu będącego częścią drzwi do lodówki.
Testowane źródła zmienności w tym przypadku były następujące:
- Linia produkcyjna do linii
- Przezbrojenie do przezbrojenia
- Panel do panelu
- Punkt pomiarowy wewnątrz panelu
Wynik badania składników zmienności możesz zobaczyć poniżej:

Interpretacja:
- Systematyczny efekt widoczny w punktach pomiarowych – litera V.
- Widoczna różnica w wynikach pomiędzy liniami produkcyjnymi – linia FMS ma wyższe wyniki.
- Brak dowodów na zmienność pomiędzy przezbrojeniami.
- Przyczyna specjalna widoczna dla panelu nr 7.
Zwiększ efektywność rozwiązywania problemów
System pomiarowy
Przykład nr 1
W tym przykładzie mamy klasyczne badanie systemu pomiarowego.
Do badania odpowiednio wybrano operatorów oraz części i każdą część (próbka) zmierzono dwa razy.
Wynik badania możesz zobaczyć poniżej:

Interpretacja:
- Dominującym źródłem zmienności jest zmienność część do części – prostokąty wyraźnie skaczą między sobą, co oznacza, że jesteśmy w stanie rozróżniać części – system pomiarowy ma odpowiednią powtarzalność.
- Dla operatora Krzysztofa i pomiarów części 6 oraz dla operatora Marka i pomiarów części 12, mamy przyczyny specjalne – wyraźnie większa różnica między pomiarami dla tych konkretnych części, co oznacza, że system pomiarowy jest nieprzewidywalny.
- Odtwarzalność jest odpowiednia – ten sam wzór dla każdego z operatorów.
- UWAGA: Patrząc na taki wykres, jestem w stanie ocenić przydatność systemu pomiarowego w różnych sytuacjach, natomiast dla wszystkich z mniejszym doświadczeniem polecam zapoznać się z formalnymi kryteriami oceny systemów pomiarowych.
Przykład 2:
Dostawca i klient nie zgadzał się co do wymiaru krytycznego profilu metalowego.
W tej sytuacji z procesu wybrano 10 części i dokonano pomiarów u dostawcy oraz klienta przy pomocy ich własnych systemów pomiarowych. Każda część została zmierzona 3 razy.
Wyniki analizy możesz zobaczyć poniżej:

Interpretacja:
- Głównym źródłem zmienności dla dostawcy jest zmienność część do części – prostokąty wyraźnie skaczą między sobą, co oznacza, że system pomiarowy ma odpowiednią powtarzalność.
- Głównym źródłem zmienności dla klienta jest zmienność pomiar do pomiaru – prostokąty zachodzą na siebie. Zmienność pomiar do pomiaru przykrywa zmienność procesu (problem precyzji).
- Wyraźne przesunięcie w średniej wyników pomiędzy dostawcą, a klientem (bias).
Planowane eksperymenty (Design of Experiments)
Przykład:
Dział R&D chciał zrozumieć wpływ 5 czynników na moc rozpraszaną przez tranzystor MOSFET.
Po przeprowadzeniu DOE (Design of Experiments), spośród 5 testowanych czynników 3 okazały się aktywne (statysycznie i praktycznie istotne).
W tym przypadku wynik eksperymentu także możemy pokazać przy pomocy Individual Value Plot:

Interpretacja:
- Efekt zmiany tranzystora to różnica między środkami największych prostokątów.
- Efekt zmiany napięcia zasilania (PowerS) to różnica między środkami średnich prostokątów.
- Efekt zmiany rezystora w bramce tranzystora (GateR) to różnica między środkami najmniejszych prostokątów.
- Efekt GateG zależy od rodzaju tranzystora MOSFET – mamy do czynienia z interakcją.
Przyśpieszone testowanie żywotności (Accelerated life testing)
Przykład
Klient miał problem jakościowy z pękającym rotorem silnika synchronicznego wykonanego z miękkiego materiału ferromagnetycznego.
Jako że silnik w normalnej pracy narażony był na nagłe zmiany temperatury, to jedna z hipotez była taka, że nagłe zmiany temperatury powodują pękanie magnesu, z którego wykonany był rotor silnika.
W celu przetestowania tej hipotezy zespół przeprowadził test (Accelerated Life Test), w którym rotor narażany był na nagłe zmiany temperatur.
Na wykresie poniżej możesz zobaczyć różnicę temperatur w zależności od ilości szoków temperaturowych.

Interpretacja:
- Uszkodzenie magnesu rotora w danych warunkach testu wystąpiło już w trzecim cyklu, przy różnicy temperatur wynoszącej 26 stopni Celsjusza.
2. Dotplot
Drugim z najczęściej używanych przeze mnie wykresów jest Dotplot.
Dotplot dzieli wartości próbek na małe przedziały i przedstawia każdą wartość lub małą grupę wartości za pomocą kropki na osi liczbowej.
Dzięki niemu możemy zrozumieć:
- Rozproszenie danych
- Położenie danych
- Najczęściej występujące wartości
- Rozkład danych
- Wielość próbki
- Wartości odstające (outliers)
Poniżej przykład przedstawiający wartości połysku jednego z lakierowanych komponentów:
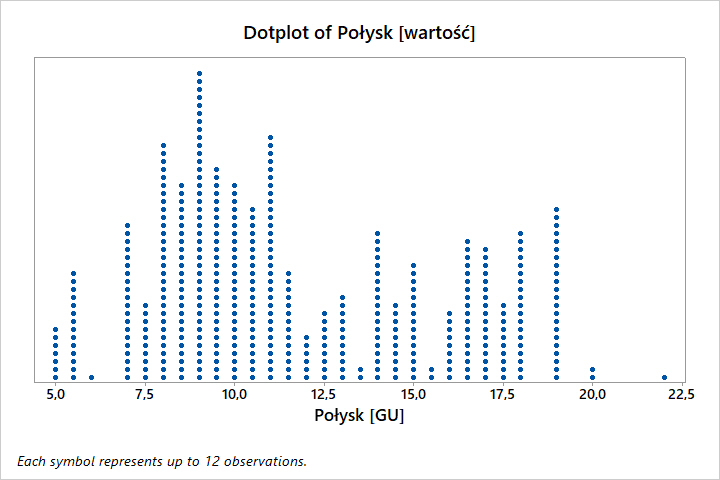
3. Histogram
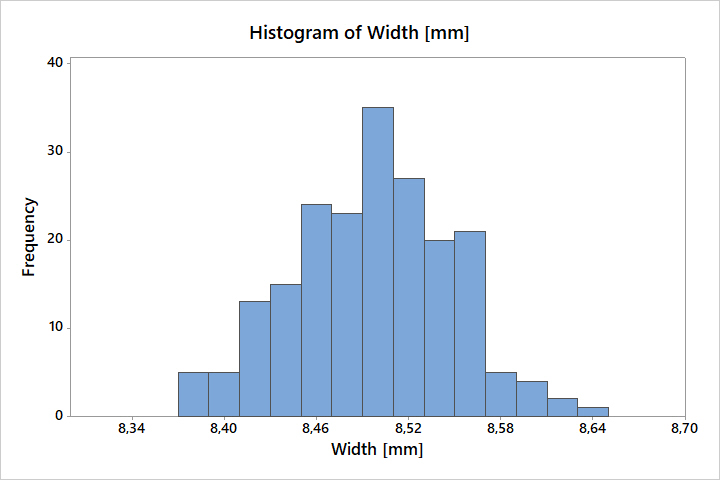
Wykresem podobnym do Dotplot jest histogram, dzięki któremu możemy zdobyć podobne informacje, jak przy Dotplot.
Histogram dzieli dane na wiele przedziałów i przedstawia częstotliwość występowania wartości w każdym przedziale za pomocą słupka.
Histogram sprawdza się lepiej przy większej ilości danych (n>100).
W jednym z kolejnych postów przedstawię Ci lepszą alternatywę dla histogramu.
4. Scatter Plot i Matrix Plot
Scatter Plot to wykres, dzięki któremu możemy zbadać związek między parą zmiennych ciągłych (X i Y).
Po utworzeniu wykresu można dodać dopasowaną linię regresji i wybrać model regresji liniowej, kwadratowej lub sześciennej.
W przykładzie poniżej możesz zobaczyć negatywną korelację (zależność) połysku komponentu od lepkości lakieru:
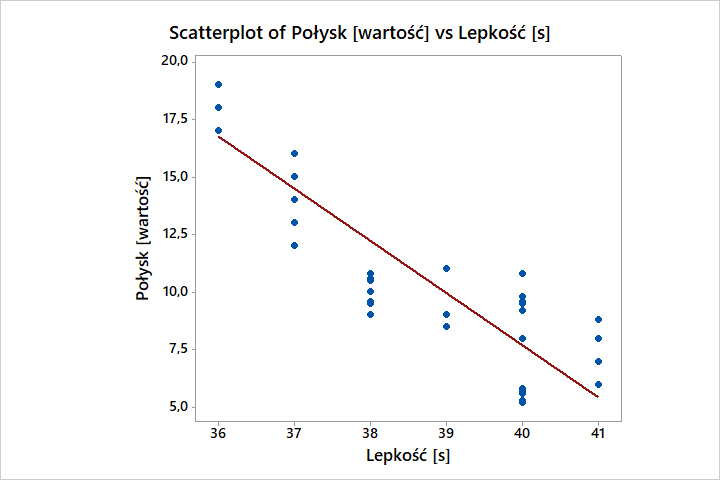
Interpretacja:
- Im większa lepkość lakieru, tym mniejszy połysk.
Rodzi się pytanie, czy istnieje związek przyczynowo-skutkowy w tej sytuacji?
Inaczej mówiąc, czy rzeczywiście jeśli zwiększymy lepkość, to czy wartość połysku się zmniejszy?
Zapamiętaj, proszę, że:
Korelacja nie oznacza przyczynowości!
Korelacja jest często powodowana przez trzeci czynnik, który nie jest widoczny w czasie badania, który nazywany czynnikiem zakłócającym. Może też występować przez czysty przypadek.
Na tej stronie zobaczysz wiele „fałszywych korelacji”, jak na przykład ta:
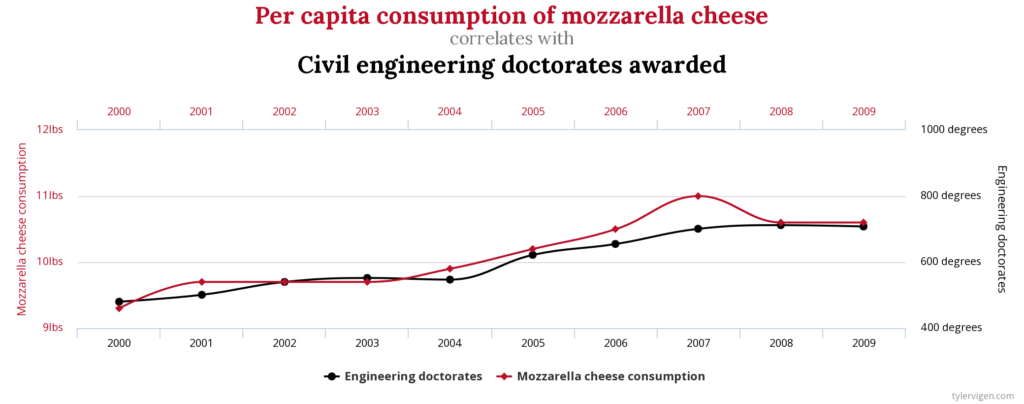
Ilość spożywanej mozzarelli jest skorelowana z ilością przyznanych doktoratów z inżynierii lądowej.
W zaprezentowanym wcześniej przykładzie zależności połysku od lepkości, po analizie danych okazało się, że mamy prawdopodobnie różną korelację w zależności od modelu komponentu.

Jedynym sposobem, aby określić czy istnieje relacja przyczyna-skutek w procesie jest przeprowadzanie eksperymentu, czyli celowej manipulacji danym czynnikiem w celu zrozumienia jego wpływu na wyjście procesu.
Najlepszą formą eksperymentowania są planowane eksperymenty (Design of Experiments), które zasługują na oddzielny post.
Warto wspomnieć o Matrix Plot, który jest matrycą wielu wykresów Scatter Plot pokazanych razem. Pozwala on ocenić zależności (korelacje) pomiędzy kilkoma parami zmiennych jednocześnie.
Poniżej możesz zobaczyć Matrix Plot dla czterech zmiennych, gdzie część górna i dolna wyświetlają te same dane, ale z odwróconymi osiami:

5. Time Series Plot
Ostatnim z najważniejszych wykresów jest Time Series Plot.
Wykres ten służy do wyszukiwania sygnałów w danych zebranych z procesu w czasie, takich jak np. przyczyny specjalne, trendy, przesunięcia, efekty cykliczne czy wzorce sezonowe.




Podsumowanie
Wykresy pozwalają na odseparowanie sygnałów od zakłóceń, które występują w danych. Dzięki temu jesteśmy w stanie podejmować odpowiednie działania zmierzające od rozwiązania problemu lub poprawy procesu.
W większości przypadków mamy dostęp do danych, lecz niestety większość nie wie jak je analizować i wyciągać wnioski, nie mówiąc o proaktywnym zbieraniu danych tak, żeby uzyskać odpowiedzi na postawione pytania.
Jest to niezwykle ważne, ponieważ rozwiązywanie złożonych problemów przy pomocy danych i analityczne (krytyczne) myślenie to dwie najważniejsze umiejętności potrzebne do funkcjonowania w czwartej rewolucji przemysłowej.
Co więcej, oprócz środowiska pracy, dane przenikają każdy aspekt naszego życia — od mediów po medycynę, od rolnictwa po finanse. Dane szybciej odpowiadają na pytania, dostarczają potrzebnych informacji i pozwalają podejmować trafniejsze decyzje.
Każdy z przedstawionych przeze mnie przykładów prowadził do konkretnych działań i jak można zauważyć, nie musieliśmy zbierać ogromnej ilości danych.
W przypadku poprawy jakości, ilość danych nigdy nie jest problemem, problemem jest zawsze ich jakość.
Co więcej, poza DOE, nie wykonałem żadnego testu statystycznego, ponieważ jego wynik nie zmieniłby kierunku moich działań.
Testy statystyczne mają swoje miejsce, lecz przy rozwiązywaniu problemów biznesowych i poprawie procesów proste metody graficzne, wiedza procesowa i ekspercka oraz praktyczne podejście są wystarczające.
Testy statystyczne, pomijając wiele założeń, które muszą spełniać, w większości przypadków są błędnie nauczane, co często skutkuje brakiem podjęcia działań.
Na koniec chciałbym Ci powiedzieć, że zbieranie danych i ich analiza to całkiem przyjemne zajęcie, szczególnie jeśli jesteś w stanie poprawić swoją kondycję, swojego pracodawcy lub klienta.
I na tym polega piękno Six Sigmy.
Zatem:
„Plot the dots” !!!
Zostaw proszę komentarz, z informacją których wykresów używasz najczęściej w swojej pracy.
Podobał Ci się wpis? Nie przegap następnego!
Zwiększ efektywność rozwiązywania problemów

Nazywam się Tomasz Leśniewicz i prowadzę SIGMA Value Consulting — butikową praktykę szkoleniowo-doradczą, której misją jest przekazywanie wiedzy na temat efektywnego rozwiązywania problemów i poprawy jakości przy użyciu danych, narzędzi Six Sigma i krytycznego myślenia.