Uważam, że w każdej organizacji (produkcyjnej i usługowej) ludzie na wszystkich poziomach powinni aktywnie wykorzystywać narzędzia, które wspierają proces ciągłego doskonalenia i rozwiązywania problemów oraz efektywniejszego podejmowania decyzji.
Jednymi z najprostszych i skutecznych narzędzi stosowanych do rozwiązywania problemów jest Siedem Podstawowych Narzędzi Jakości, znanych także jako Wspaniała Siódemka.
Wielkim zwolennikiem i promotorem tych narzędzi był sławny dr Kaoru Ishikawa — twórca diagramu przyczynowo-skutkowego, który w 1985 roku stwierdził, że: „95% problemów w procesach można rozwiązać za pomocą siedmiu narzędzi kontroli jakości (QC)”.
Moje doświadczenia we współpracy z różnymi organizacjami i klientami oraz badania pokazują, że dzisiejsze problemy są jednak bardziej skomplikowane i często podstawowe narzędzia ze wspaniałej siódemki już nie wystarczają.
Być może nadszedł czas, aby ponownie przyjrzeć się roli i wkładowi Siedmiu Podstawowych Narzędzi Jakości w rozwiązywaniu problemów i poprawie procesów w dzisiejszych czasach (organizacjach?). Na tym przecież polega ciągłe doskonalenie…
W tym artykule chciałbym Ci zaproponować nowe spojrzenie na Siedem Głównych Narzędzi Jakości, dzięki czemu Twoja efektywność w rozwiązywaniu problemów i poprawie procesów wzrośnie.
Zapraszam do lektury.
Zawartość artykułu
Siedem Podstawowych Narzędzi Jakości - krótki opis
HISTOGRAM
Histogram dzieli dane na wiele przedziałów i przedstawia częstotliwość występowania wartości w każdym przedziale za pomocą słupka.
DIAGRAM PRZYCZYNOWO-SKUTKOWY
(DIAGRAM ISHIKAWY)
Diagramy przyczyn i skutków identyfikuje i kategoryzuje wiele potencjalnych przyczyn danego efektu lub problemu.
SCHEMAT BLOKOWY
Schemat blokowy jest graficznym przedstawieniem procesu, pokazującym kolejność wykonywania zadań.
WYKRES PARETO
Wykres Pareto to typ wykresu, który zawiera zarówno słupki, jak i wykres liniowy, gdzie poszczególne wartości są reprezentowane w porządku malejącym za pomocą słupków, a skumulowana suma jest reprezentowana przez linię.
ARKUSZ KONTROLNY
Arkusz kontrolny to ustrukturyzowany, przygotowany formularz do zbierania danych.
KARTA KONTROLNA
Karta kontrolna to wykres używany do badania przewidywalności zachowania procesu (zmienność naturalna vs specjalna).
WYKRES KORELACJI
Wykres korelacji to wykres, dzięki któremu możemy zbadać związek między parą zmiennych ciągłych (X i Y).
O tym, czym jest Problem Solving, jaki jest proces i czego potrzebujemy, aby efektywnie rozwiązywać problemy, możesz przeczytać tutaj: Problem Solving, czyli rozwiązywanie problemów wszelakich dla początkujących
HISTOGRAM + CDF = idealna para
Histogram dzieli dane na wiele przedziałów i przedstawia częstotliwość występowania wartości w każdym przedziale za pomocą słupka (binu).
Dzięki niemu możemy zrozumieć:
- Rozproszenie danych
- Położenie danych
- Najczęściej występujące wartości
- Rozkład danych (więcej informacji na ten temat znajdziesz w dalszej części artykułu)
Świetnym uzupełnieniem histogramu jest wykres dystrybuanty (Cumulative Density Function, CDF) – ma on kilka zalet, które sprawiają, że warto się z nim zapoznać.
Bezpośredni odczyt podstawowych wartości
Jedną z głównych zalet CDF w stosunku do histogramu jest fakt, że mogące Cię interesować wartości takie jak np. minimum, maksimum, mediana, kwantyle, percentyle, mogą być bezpośrednio odczytane z wykresu.
Histogram i wykres CDF dla przykładowego zestawu danych, możesz zobaczyć poniżej:


Wykrywanie potencjalnych przyczyn specjalnych lub outlierów
Czym są przyczyny specjalne i dlaczego ich identyfikacja jest bardzo ważna możesz przeczytać w poniższym artykule:
W niektórych przypadkach wykrycie wartości odstających na histogramie może być trudne, ponieważ łatwo je przeoczyć, jak w sytuacji poniżej:
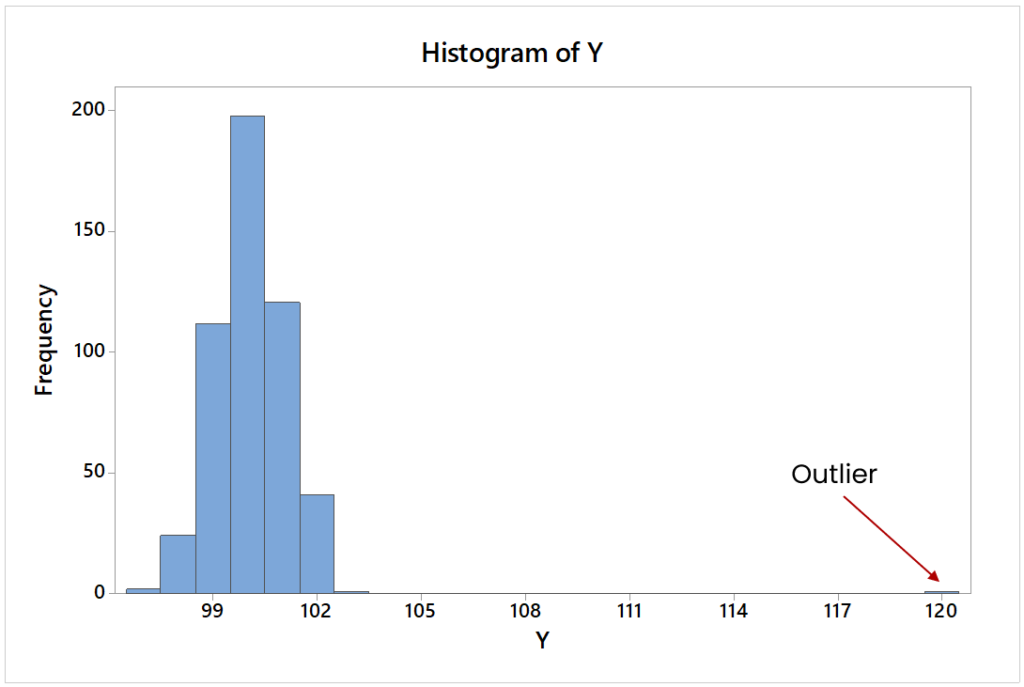
CDF dla tego przykładu będzie następujący:
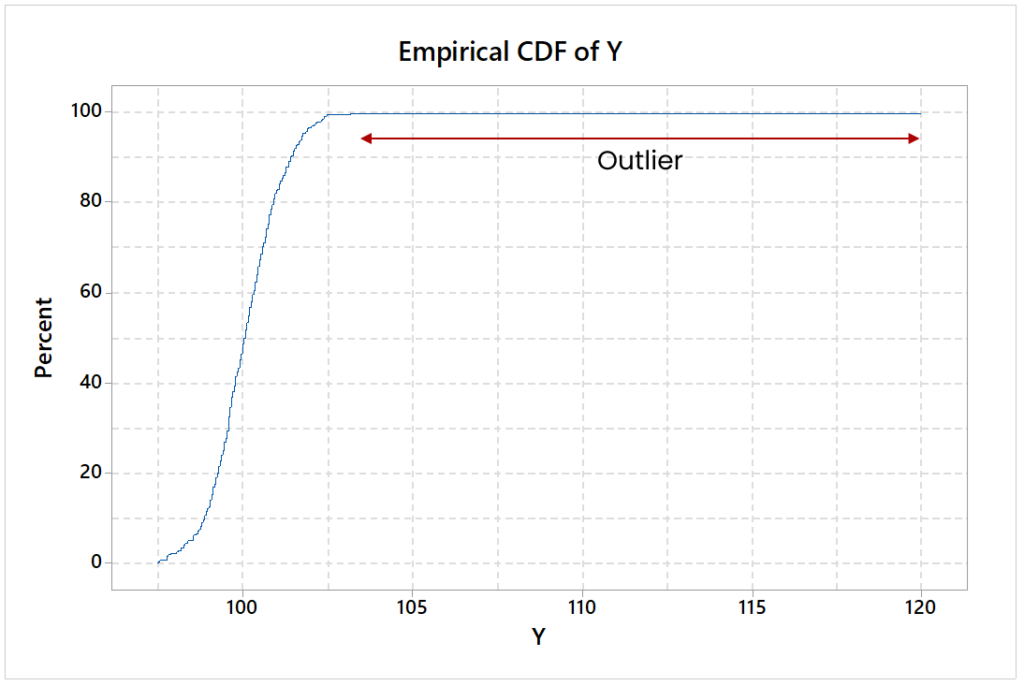
Identyfikacja rozkładu danych
Korzystając z CDF, możemy także zidentyfikować model, jakim możemy opisać nasze dane, np. rozkład normalny, jak poniżej:
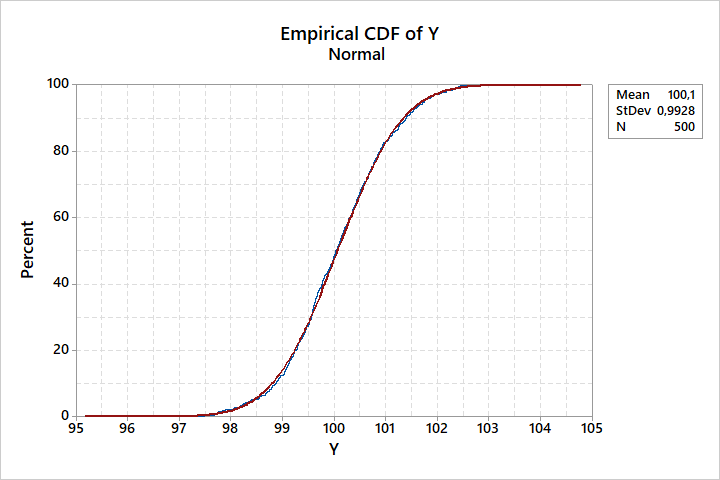
Im lepsze pokrycie rzeczywistych danych (linia niebieska) z modelem (linia czerwona), tym lepiej model reprezentuje nasze dane.
Przewaga nad histogramem jest taka, że w przypadku CDF jesteśmy niewrażliwi na wszelkiego rodzaju manipulacje przy histogramie, jak np. ustawienia ilości binów, które to mogą zmienić naszą interpretację rodzaju rozkładu danych.
Porównanie kilku zbiorów danych
Dzięki CDF bardzo łatwo możemy porównywać wiele zbiorów danych i odczytywać interesujące nas informacje.
Porównanie wielu zbiorów danych na wykresie jest zdecydowanie łatwiejsze przy wykorzystaniu CDF. Dzięki temu łatwiej też odczytać interesujące nas wartości z poszczególnych zbiorów.

Odporność na manipulację
Nie ma „najlepszej” liczby przedziałów na histogramie, a ich różna liczba wpływa na jego interpretacje.
Jeśli jest zbyt mało przedziałów, wykres będzie nieprecyzyjny i nie będzie dobrze przedstawiał danych. Jeśli będzie zbyt wiele przedziałów, wiele z nich będzie niezajętych, co znowu wpłynie na naszą błędną interpretację.
Poniższe histogramy przedstawiają te same dane z różną liczbą przedziałów.
Jak widzisz, każdy z nich możesz zinterpretować inaczej.

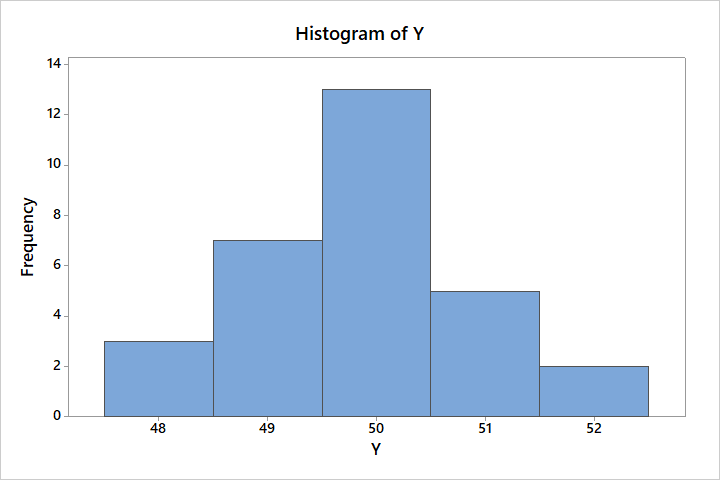

Taka sytuacja nie występuje, kiedy używamy CDF:

Z diagramu Ishikawy i schematu blokowego do MAPY PROCESU
Diagram Ishikawy (diagram rybiej ości) to narzędzie służące do graficznego przedstawienia związku między skutkiem (np. problemem lub kluczową cechą), a potencjalnymi przyczynami, które na niego wpływają.

W Internecie znajdziesz wiele stron prezentujących to narzędzie. Ja natomiast chciałbym się skupić nad ograniczeniami Ishikawy, a później na zaproponowaniu Ci alternatywy.
Jakie są zatem główne ograniczenia diagramu Ishikawy? Przede wszystkim nie znamy odpowiedzi na poniższe pytania, które są zawsze kluczowe w kontekście poprawy procesów:
- Jaki jest cel procesu, w którym wystąpił problem?
- Jakie są cele poszczególnych operacji lub etapów procesu?
- Jakie są małe „y” (dane wyjściowe z pojedynczego kroku, operacji lub fazy procesu), które przyczyniają się do realizacji dużego „Y”?
- Która z potencjalnych przyczyn (czynników) jest kontrolowana?
- Jakie są zakresy, w których operują czynniki, które kontrolujemy (poziom nominalny i wartości skrajne)?
- Dla tych, które są kontrolowane, czy mamy jakieś doświadczenia potwierdzające potencjalną relację przyczyna-skutek?
- Które z czynników nie kontrolujemy, dlatego że nie wiemy, czy są istotne lub techniczne/ekonomicznie jest to nieuzasadnione?
- Co wiemy o potencjalnej relacji między czynnikami (interakcje)?
- Gdzie są obecnie gromadzone dane?
Odpowiedzi na te pytania możemy dostać, tworząc narzędzie, które będę nazywał Mapą Procesu.
Mapa Procesu to połączenie schematu blokowego, diagramu Ishikawy oraz wiedzy o tym, jak proces jest zarządzany.
Mapowanie procesów jest graficznym przedstawieniem związków przyczynowo-skutkowych, co pozwala na zdobywanie wiedzy na temat zachowania procesu, tak aby kontrolować proces w przewidywalny sposób z minimalną zmiennością.
Mapy Procesu dokumentują obecną wiedzę na temat procesów i stymulują potrzebę gromadzenia tej wiedzy.
Poniżej możesz zobaczyć przykładową Mapę Procesu dla oznaczania pierwiastków chemicznych w próbkach przy pomocy absorpcyjnej spektrometrii atomowej (AAS):

Na tej Mapie Procesu możesz zauważyć kilka oznaczeń.
Duży „Y” opisuje liczbowo zjawisko, które nas interesuje i odnosi się do zakresu realizowanego projekt — chcemy być w celu z minimalną zmiennością.
Dla każdego kroku procesu możesz zobaczyć potencjalne czynniki, które wpływają na wyjście procesu, czyli Twój duży „Y”.
Każdy z nich przypisujemy do przynajmniej dwóch podstawowych kategorii:
C (controllable) – czynniki, którymi manipulujemy w procesie. Jeśli np. istnieje możliwość wyboru źródła surowca czy ustawienia parametrów maszyny/urządzenia, to jest to kontrolowany x.
N (noise) – czynniki, których obecnie nie kontrolujemy, ponieważ nie wiemy, czy są ważne lub ich kontrolowanie jest techniczne/ekonomicznie nieuzasadnione. Tego rodzaju czynniki nazywamy po prostu zakłóceniami. Może to być związane z surowcami, środowiskiem lub nieustandaryzowanymi praktykami operacyjnymi.
W praktyce ta ostatnia kategoria może być najważniejsza, ponieważ reprezentuje czynniki, o których wiemy najmniej. To często powód, dlaczego w procesach mamy problemy jakościowe — nie rozumiemy, jak zakłócenia wypływają na wyjście.
Często też nie jesteśmy w stanie znaleźć klasycznymi metodami eksperymentowania skomplikowanych interakcji między czynnikami zakłócającymi a tymi, którymi manipulujemy.
Gdyby relacje procesów były naprawdę deterministyczne, wiedza na temat zakłóceń nie byłaby konieczna. Dlatego tak ważne jest zrozumienie, jak zakłócenia wpływają na nasze procesy. Jeśli się tego dowiesz i okaże się, że stopień wpływu zakłócenia jest praktycznie istotny to albo musisz zacząć je kontrolować, albo się na nie uodpornić (robust design).
Zrozumienie jak zakłócenia wpływają na proces, jest jedną z najważniejszych rzeczy, dzięki której poprawiamy jakość i rozwiązujemy problemy.
Korzyści z mapy procesu:
- Identyfikacja kluczowych metryk charakteryzujących problem
- Identyfikacja wejścia/wyjścia/klientów
- Lepsze zrozumienie procesu i jego celu
- Identyfikacja miejsc pomiarów
- Identyfikacja potencjalnych przyczyn problemu
- Organizowanie listy potencjalnych przyczyn i zrozumienie, do jakich głównych źródeł zmienności należą (rate of change table)
- Powiązanie wyników procesu z parametrami procesu
- Identyfikacja obszarów wymagających poprawy
- Zapewnienie lepszej komunikacji pomiędzy grupami
- Dane wejściowe do DOE
Wiedza o procesie może być opisana przez zestaw równań Y = f(x) + N.
Informacje te mogą być następnie wykorzystane do kontroli procesu w celu osiągnięcia wymaganego poziomu procesu (położenia) i zmniejszenia zmienności. Prezentowana Mapa Procesu jest nieodzownym narzędziem, które pozwala szybciej i bardziej efektywnie rozwiązywać problemy i poprawiać procesy.
Zwiększ efektywność rozwiązywania problemów
WYKRES PARETO (ale ze świadomością jego ograniczeń)
Wykres Pareto to podstawowe narzędzie jakości, które pomaga zidentyfikować najczęstsze defekty, reklamacje lub inne czynniki, które możesz policzyć i skategoryzować.
Wykres wziął swoją nazwę od Vilfredo Pareto, twórcy „reguły 80/20”, która zakłada, że z grubsza:
„80 procent efektów pochodzi z 20 procent przyczyn”
Odnosząc to do życia codziennego, możemy znaleźć poniższe przykłady, w których ta zasada obowiązuje:
- 80% pieniędzy pochodzących z podatków pochodzi od około 20% społeczeństwa
- 80% efektu wynika z 20% wysiłku
- 80% dochodów pochodzi od 20% ich klientów
- 80% awarii systemu jest spowodowanych przez 20% błędów
- 80% wszystkich wypadków drogowych jest powodowanych przez 20% kierowców
- 80% zanieczyszczeń pochodzi z 20% wszystkich fabryk
- 80% sprzedaży jest generowanych przez 20% produktów
- 80% wyników jest realizowanych przez 20% pracowników
Wykres Pareto to po prostu wykres słupkowy, który porządkuje słupki (liczby) od największego do najmniejszego, od lewej do prawej. Kategorie lub czynniki symbolizowane przez większe słupki po lewej stronie są ważniejsze niż te po prawej stronie.
Możesz użyć wykresu Pareto za każdym razem, gdy masz dane podzielone na kategorie i możesz policzyć, jak często występuje każda kategoria, jak na przykładzie poniżej:

Niestety taki standardowy wykres nie jest najlepszą formą prezentowania tego rodzaju danych.
Poniżej możesz zobaczyć wersję poprawioną, która jest zdecydowanie bardziej czytelna:

Chociaż wykres Pareto jest łatwy do stworzenia, zrozumienia i użycia, ma pewne ograniczenia:
- Dane zbierane w krótkim czasie, zwłaszcza z niestabilnego procesu, mogą prowadzić do błędnych wniosków. Jeśli dane nie są wiarygodne, możesz uzyskać błędny obraz rozmieszczenia defektów.
- Dane gromadzone przez długi czas mogą obejmować zmiany wprowadzone w procesie, dlatego warto sprawdzić, czy są jakieś sygnały w danych zbieranych w czasie.
- Upewnij się, że wybrałeś sensowne kategorie defektów – często największą kategorią jest kategoria „inne”.
- Nie zawsze największa ilość np. defektów danej kategorii jest tym, co najbardziej boli klientów lub generuje największe straty dla organizacji.
- Upewnij się, że każda kategoria ma konkretną definicję operacyjną.
- Uważaj na problemy z systemem pomiarowym.
- Nie myl wykresu Pareto ze zrozumieniem relacji przyczynowo-skutkowej Y=f(x).
- Bądź świadom kto, gdzie, kiedy i w jakich warunkach zbierał dane.
- Weź pod uwagę rodzaj zmienności (naturalna vs specjalna), kiedy analizujesz dane. Inaczej mówiąc, czy defekty zostały wygenerowane przez przewidywalny proces, czy proces niestabilny.
Od arkuszy kontrolnych do REJESTRATORÓW ZDARZEŃ
Arkusz kontrolny to ustrukturyzowany, przygotowany formularz do zbierania i analizowania danych najczęściej w formie analogowej.
Poniżej możesz zobaczyć przykład takiego arkusza do zbierania danych ciągłych:
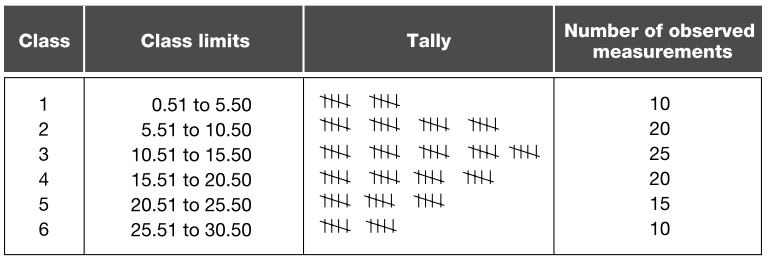
Informacje uzyskane z zebranych danych oraz skuteczność decyzji podjętych na podstawie uzyskanych pomiarów zależą w dużej mierze od planowania strategii zbierania danych.
W większości organizacji gromadzona i przechowywana jest duża ilość danych historycznych. Często dane historyczne nie zawierają informacji, które są znaczące lub przydatne jako podstawa do podejmowania decyzji.
Aby uzyskać istotne informacje z danych, należy opracować strategię gromadzenia danych opartą na dokładnym opisie procesu (Mapa Procesu) i potencjalnych czynnikach, które wpływają na wyniki procesu. Strategia gromadzenia danych dyktuje mierzone cechy jakościowe, punkt w procesie, w którym pomiar ma się odbyć, oraz rodzaj gromadzonych danych.
Arkusz kontrolny, który pomaga w uzyskaniu informacji potrzebnych do poprawy procesu, jest opracowywany dopiero po dokładnym zrozumieniu procesu i identyfikacji potencjalnych czynników przyczynowych. Bardzo prawdopodobne jest, że „pozycje” na arkuszu zostaną usunięte lub dodane w miarę zdobywania wiedzy o procesie, rozwiązywania pewnych problemów oraz odkrywania i definiowania nowych problemów klientów.
Pytanie tylko jaka forma takiego arkusza kontrolnego jest najlepsza? Arkusz kontrolny powinien zapewniać, że zbieranie danych będzie szybkie, wymagające mało wysiłku, odporne na błędy, z możliwością otrzymania podsumowania, łatwej archiwizacji i późniejszego szybkiego dostępu do danych w celu analizy.
Na pewno arkusz kontrolny w formie papierowej, gdzie dane są zbierane manualnie, nie spełnia tych kryteriów.
W dobie smartfonów, tabletów, IoT nie jest to jednak problem, ponieważ proces zbierania danych możemy zdigitalizować, zapisując dane w formie cyfrowej lub korzystając z dedykowanych systemów jak np. SCADA (ang. Supervisory Control And Data Acquisition) – system informatyczny nadzorujący przebieg procesu technologicznego lub produkcyjnego. Jego główne funkcje obejmują zbieranie aktualnych danych (pomiarów), ich wizualizację, sterowanie procesem, alarmowanie oraz archiwizację danych.
Można też skorzystać z coraz bardziej popularnych platform programistycznych bez kodu (NCDP) do rejestrowania i przetwarzania danych.
KARTA KONTROLNA - bez zmian
Z mojego doświadczenia wynika, że niewiele organizacji czerpie korzyści z tego narzędzia. Prawdopodobnie wynika to z braku zrozumienia mechaniki jej działania.
Jeśli chcesz wiedzieć, czym jest karta kontrolna i jakie są korzyści z jej używania, to zapraszam do mojego artykułu:
Z wykresu korelacji (Scatter Plot) i Matrix Plot do PRINCIPAL COMPONENTS ANALYSIS
Czym jest wykres korelacji (Scatter Plot) i Matrix Plot dowiesz się z mojego wcześniejszego artykułu:
Tego rodzaju wykresy są efektywne, gdy mamy nie więcej niż około 15-20 zmiennych, a co gdy takich czynników masz więcej? To szczególnie istotnie, ponieważ obecnie urządzenia dostarczają masę informacji, których możemy użyć do poprawy procesów.
W takiej sytuacji możesz skorzystać z Principal Components Analysis.
Analiza PCA to matematyczna procedura, która przekształca pewną liczbę (prawdopodobnie) skorelowanych zmiennych w (mniejszą) liczbę nieskorelowanych zmiennych zwanych głównymi składnikami.
Pierwszy główny składnik odpowiada za jak największą zmienność danych, a każdy kolejny składnik odpowiada za jak największą część pozostałej zmienności.
Główną ideą analizy PCA jest zmniejszenie wymiarowości zbioru danych.
Poniżej możesz zobaczyć rzeczywisty przykład dla 5 zmiennych. Jak widzisz, są one ze sobą skorelowane:
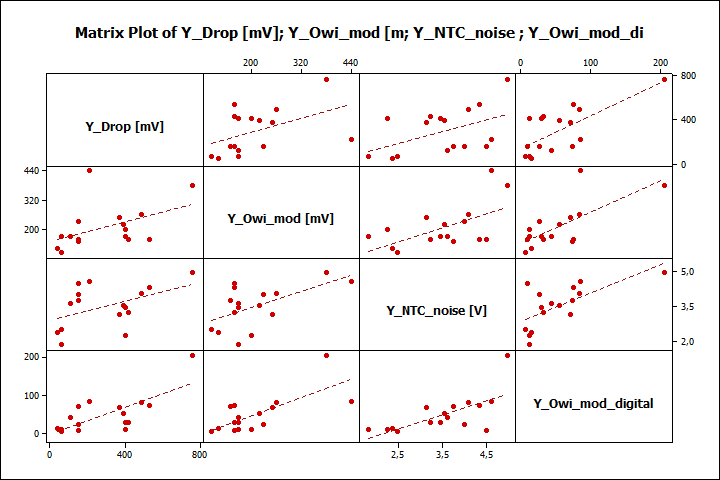
Po przeprowadzeniu analizy PCA identyfikujemy liczbę komponentów, które wyjaśniają większość zmienności w naszych danych.
Jak możesz zobaczyć poniżej, większość zmienności może być reprezentowana przez pierwszy główny komponent.


Następnie możemy określić, które zmienne mają największy wpływ na każdy komponent.
Do tego celu używamy wykresu Loading Plot. Loading mogą wynosić od -1 do 1. Wartości -1 lub 1 wskazują, że zmienna silnie wpływa na komponent, a Loading bliskie 0 wskazują, że zmienna ma słaby wpływ na składnik.
Dla przykładu powyżej największy wpływ na pierwszy komponent ma Y_Owi_mod_digital.
Widzimy też pozytywną korelację Y_Drop z komponentem drugim oraz negatywną korelację Y_NTC_noise i Y_Owi_mod także z komponentem drugim — dzięki temu wiem jakie metryki są reprezentowane przez poszczególne komponenty.
Takie podejście pozwala nam na zredukowanie naszych zmiennych na przykład podczas eksperymentowania.
Następnie możemy zobaczyć, jak każda metryka wpływa na dany komponent. Wykres Landing Plot pokazuje, jak silnie każda metryka jest skorelowana z danym komponentem.
Kąty między wektorami mówią nam, jak korelują ze sobą cechy.
Podsumowanie
Siedem podstawowych narzędzi jakości powinien znać każdy członek organizacji, która na poważnie myśli o budowaniu kultury organizacji „uczącej się” i ciągłego doskonalenia.
Wydaje mi się jednak, że opracowany kilka dekad temu podstawowy zestaw nie odpowiada czasom, w których się znaleźliśmy.
Przy dzisiejszych możliwościach komputerów i zautomatyzowanej akwizycji danych możemy być bardziej efektywni w rozwiązywaniu problemów, dodając do podstawowego zestawu kilka nowych prostych narzędzi lub łącząc podstawowe narzędzia ze sobą i tworząc np. Mapę Procesu.
Dużo się teraz mówi o przywództwie, deprecjonując narzędzia i odsuwając je na dalszy plan.
Jednak bez znajomości choćby podstawowych narzędzi, nie będziemy w stanie poprawiać żadnych procesów i rozwiązywać problemów tak efektywnie, jak z ich znajomością.
Stan ten należy zmienić poprzez ciągłą edukację i szkolenia personelu.
A czy Ty używasz Siedmiu Podstawowych Narzędzi Jakości w ich podstawowej, czy zmodyfikowanej formie?
Podobał Ci się wpis? Nie przegap następnego!
Zwiększ efektywność rozwiązywania problemów

Nazywam się Tomasz Leśniewicz i prowadzę SIGMA Value Consulting — butikową praktykę szkoleniowo-doradczą, której misją jest przekazywanie wiedzy na temat efektywnego rozwiązywania problemów i poprawy jakości przy użyciu danych, narzędzi Six Sigma i krytycznego myślenia.